Модель с настраиваемым параметром матричного предиктора

Решающим фактором выбора модели с настраиваемым параметром матричного предиктора, является не число наблюдений, а, скорее, ситуация, когда за рамками системы показателей, для которых строится матричный предиктор остались факторы, оказывающие заметное влияние на динамику. Природа этих факторов либо не изучена, либо такова, что не поддаётся количественному измерению, и поэтому факторы не могут быть включены в модель. Но их влияние проявляется в динамике показателей, включённых в модель. Уловить это влияние можно, если прирост каждого показателя разделить на две части, одна из которых формируется механизмом, явно учитываемым моделью, а вторая – «скрытыми» факторами. В соответствии с этим делением прирост представляется в виде суммы двух составляющих [4]:

,

где – часть прироста, которая формируется «скрытыми» факторами;

– часть прироста, которая формируется пропорционально факторам, включённым в модель.

Поскольку влияние «скрытых» факторов в соответствии с нашим предположением проявляется непосредственно в динамике самих показателей, то и отразить это влияние можно через собственные темпы той части прироста, которая формируется «скрытыми» факторами, т.е.:

.

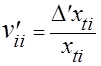Коэффициенты косвенных темпов прироста в этом случае называются частными и вычисляются по второй составляющей прироста:

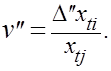
Сложение диагональной матрицы прямых темпов прироста:

,

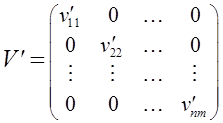элементы которой вычислены по формуле , и матрицы косвенных темпов прироста с элементами :

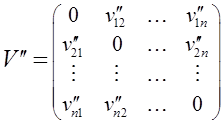
приводит к матрице темпов прироста

,

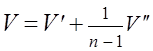с помощью которой можно записать

где матрица роста с элементами, представляющими собой частные коэффициенты роста.

Для определения отношения, в котором находятся две составляющие прироста, в модель необходимо ввести настраиваемый параметр. Это возможно тогда, когда имеются данные более двух наблюдений, часть которых можно использовать в качестве контрольной выборки для настройки параметра.

Введение такого параметра позволяет каждую из составляющих прироста любого -го показателя представить виде:

где .

Если в формулах и используются составляющие прироста, , то матрица темпов приростов зависит от настраиваемого параметра и модель можно переписать в виде:

Читайте также:

Использование страхования залогового автомобиля
Страхование предлагается банками в качестве обязательного обеспечения при продаже автомобилей в кредит физическим лицам, а также частным предпринимателям без образования юридического лица. Страхование осуществляется на основе трехстороннего соглашения между банком, страховой компанией и автосалоном ...

Современные формы кредитования физических лиц в Российской Федерации
С начала этого года рынок кредитования физических лиц постепенно восстанавливается. В прошлом году спрос на кредиты в России падал в силу целого ряда факторов. Это и снижение официальных и реальных доходов потенциальных заемщиков и их страхи по поводу завтрашнего дня, но, безусловно, одной из важне ...

Анализ финансово-хозяйственной деятельности ООО "Росгосстрах - Татарстан"
На втором этапе проведем анализ финансово-хозяйственной деятельности ООО "Росгосстрах-Татарстан". Рассмотрим текущее позиционирование Нижнекамского городского филиала ООО "Росгосстрах-Татарстан" на рынке. Нижнекамский городской филиал входит в группу филиалов Общества с ограниче ...