Методы изучения взаимосвязи между явлениями

Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. [12]

В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и регрессионного анализа. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого. [12]

Основными задачами корреляционного анализа являются: оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Для измерения тесноты связи меду двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяется парный коэффициент корреляции. Если известны средние квадратические отклонения (σ) анализируемых величин, то парные коэффициенты корреляции рассчитывают по формулам:

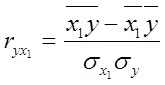; (13)

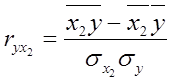; (14)

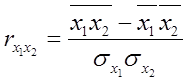. (15)

В реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляциями, которые характеризуют степень и влияние одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. Частный коэффициент корреляции первого порядка между признаками x1 и y при исключении влияния признака x2 вычисляют по формуле:

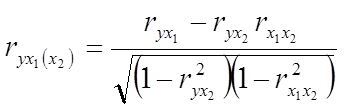; (16)

то же – зависимость y от x2 при исключении влияния x1.

Показателем тесноты связи, устанавливаемой между результативным и двумя или более факторными признаками, является совокупный коэффициент множественной корреляции 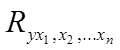. В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции может быть рассчитан по формуле:

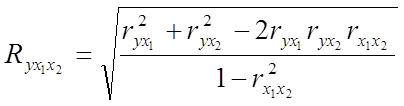, (17)

где r – линейные коэффициенты корреляции (парные); подстрочные индексы показывают, между какими признаками они исчисляются.

Совокупный коэффициент множественной корреляции измеряет одновременное влияние факторных признаков на результативный. Его значения находятся в пределах -1 до +1. Чем меньше наблюдаемые значения изучаемого показателя отклоняются от линии множественной регрессии, тем корреляционная связь интенсивнее, а следовательно, значение R ближе к единице. [11]

Величина R2, которая показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии, называется совокупным коэффициентом множественной детерминации. Значение совокупного коэффициента множественной детерминации находится в пределах от 0 до 1. Поэтому, чем ближе R2 к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов. [7]

Показатели множественной регрессии и корреляции могут оказаться подверженными действию случайных факторов. Общую оценку адекватности уравнения получают с помощью дисперсионного F-критерия Фишера:

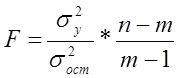, (18)

где m – число параметров в уравнении регрессии.

Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

Уравнение однофакторной регрессионной связи имеет вид:

, (19)

где – теоретические значения результативного признака;

а0 и а1 – параметры уравнения регрессии.

При исследовании влияния на результативный фактор нескольких факторных применяется формула множественной регрессии с n-факторами:

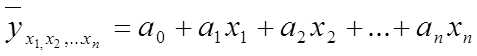(20)

Чтобы иметь представление о силе влияния отдельных факторных признаков на результативный, вычисляют следующие коэффициенты:

Коэффициент эластичности:

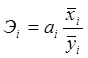, (21)

где - коэффициент регрессии при i-ом факторе, - среднее значение i-го фактора, - среднее значение результативного признака.

Читайте также:

Анализ системы ипотечного кредитования
В целях развития ипотечного кредитования строящегося жилья в 2010 году Банк пересмотрел требования по аккредитации объектов застройщиков, что позволило существенно расширить перечень потенциальных объектов для оформления кредита без промежуточного залога. Важным шагом в 2010 году стал запуск акции ...

Оценка кредитоспособности ООО «ЗСС» по предложенным рекомендациям
Определим новую методику оценки кредитоспособности ООО «ЗСС» на 2009 год с помощью расширенного метода рейтинговой оценки. В данной методике будет рассмотрено 27 позиций надежности заемщика. С правой стороны от результатов будут проставлены баллы. Максимальный балл 20, минимальный балл 0. Общее кол ...

Основные направления по успешному развитию банковской деятельности
коммерческий операция банк Можно выделить два основных направления, по которым должно происходить качественное совершенствование банковской сферы и ее деятельности. Первое – развитие процессов концентрации в банковском деле. Это связано с тем, что банки должны сыграть ключевую роль в финансовом обе ...